Newton Method 2

前回の記事の続き。

関数$f$が狭義凸関数であるときにヘッセ行列が正則になる証明を行っていく。以下では、ヘッセ行列の各成分は実数であるとする。

流れ

先に証明の流れを書いておく。

１. 正定値対称行列が正則であることを証明する

２. ヘッセ行列が正定値対称行列であることを証明する
２.１. 狭義凸関数の性質である

\[f(x) > f(a) + \nabla f(a)^T (x - a)\]

を証明する。

２.２. $f$を2次のテーラー展開して、ヘッセ行列が式中に現れることを確認する。

\[f(x) = f(a) + \nabla f(a)^T(x - a) + \frac{1}{2}(x - a)^T Hf(c)(x - a)\ \ \ \ (\exists{c}, c\in {\lambda x + (1 - \lambda)y, 0\le \lambda \le 1})\]

２.３.下の式が導けるので、凸関数の性質からヘッセ行列が正定値であることが証明される

\[\frac{1}{2}(x - a)^T Hf(c)(x - a) = f(x) - f(a) - \nabla f(a)^T(x - a) > 0\]

正定値対称行列が正則であることの証明

まず正定値対称行列について。

$n\times n$行列$A$が長さ$n$の任意の実数値ベクトル$z$について、$z^TAz > 0$を満たすとき、$A$を正定値行列(positive definite matrix)という¹。更に、正定値行列$A$が対称行列であるときその行列$A$は正定値対称行列であるという。

$A$は対称行列であるので、その成分が実数であるとき対角化可能。よって、適当な直交行列$P$と対角行列$D$を用いて、

\[A = P^TDP\]

のように表せる。ここで、任意のベクトル$z (z\in\mathbb{R^n})$を用いると、

\[\begin{align} z^TAz &= z^TP^TDPz\\ &= (Pz)^TDPz\\ &= y^TDy\ \ \ (y := zP)\\ &= \sum_{i=1}^n y_i^2d_i > 0 \tag{1} \end{align}\]

のように式変形できる(最後の不等号は正定値行列の定義より)。 $y$が任意のベクトルであることから、$(1)$式より$A$を対角化した行列の対角成分は全て正であることが分かる。

さて、$A$の行列式を考えると、

\[\begin{align} det(A) &= det(P^{-1}DP)\\ &= det(P^{-1})det(D)det(P)\\ &= det(P)^{-1}det(D)det(P)\\ &= det(D)\\ \end{align}\]

対角行列の行列式はその対角成分の積であるので、行列式は正。よって正則である。

ヘッセ行列が正定値対称行列であることの証明

狭義凸関数の性質である

\[f(x) > f(a) + \nabla f(a)^T (x - a) \tag{2}\]

を証明する。

狭義凸関数の性質より、

\[f((x+y)/2) < \frac{1}{2}f(x) + \frac{1}{2}f(y)\]

$h:= y - x$とおくと、

\[f(x+h/2) < \frac{1}{2}f(x) + \frac{1}{2}f(x + h)\\\]

これを式変形すると、

\[\begin{align} f(x + h) - f(x) &> \frac{f(x+h/2) - f(x)}{1/2}\\ &> \frac{\frac{f(x+h/4) - f(x)}{1/2}}{1/2} = \frac{f(x+h/4) - f(x)}{1/4}\\ \dots\\ &> \frac{f(x+2^{-k}h) - f(x)}{2^{-k}}\\ \end{align}\]

が任意の$k\in\mathbb{N}$で成り立つことが分かる。よって微分の定義より、

\[\begin{align} f(x + h) - f(x) &> \lim_{k\rightarrow \infty}\frac{f(x+2^{-k}h) - f(x)}{2^{-k}}\\ &= \lim_{k\rightarrow \infty}\frac{f(x+2^{-k}h) - f(x)}{2^{-k}h}h\\ &= \nabla f(x)^{T}h\\ \end{align}\]

証明できた。

ところで、この式は感覚的にも分かりやすい式であると思う。

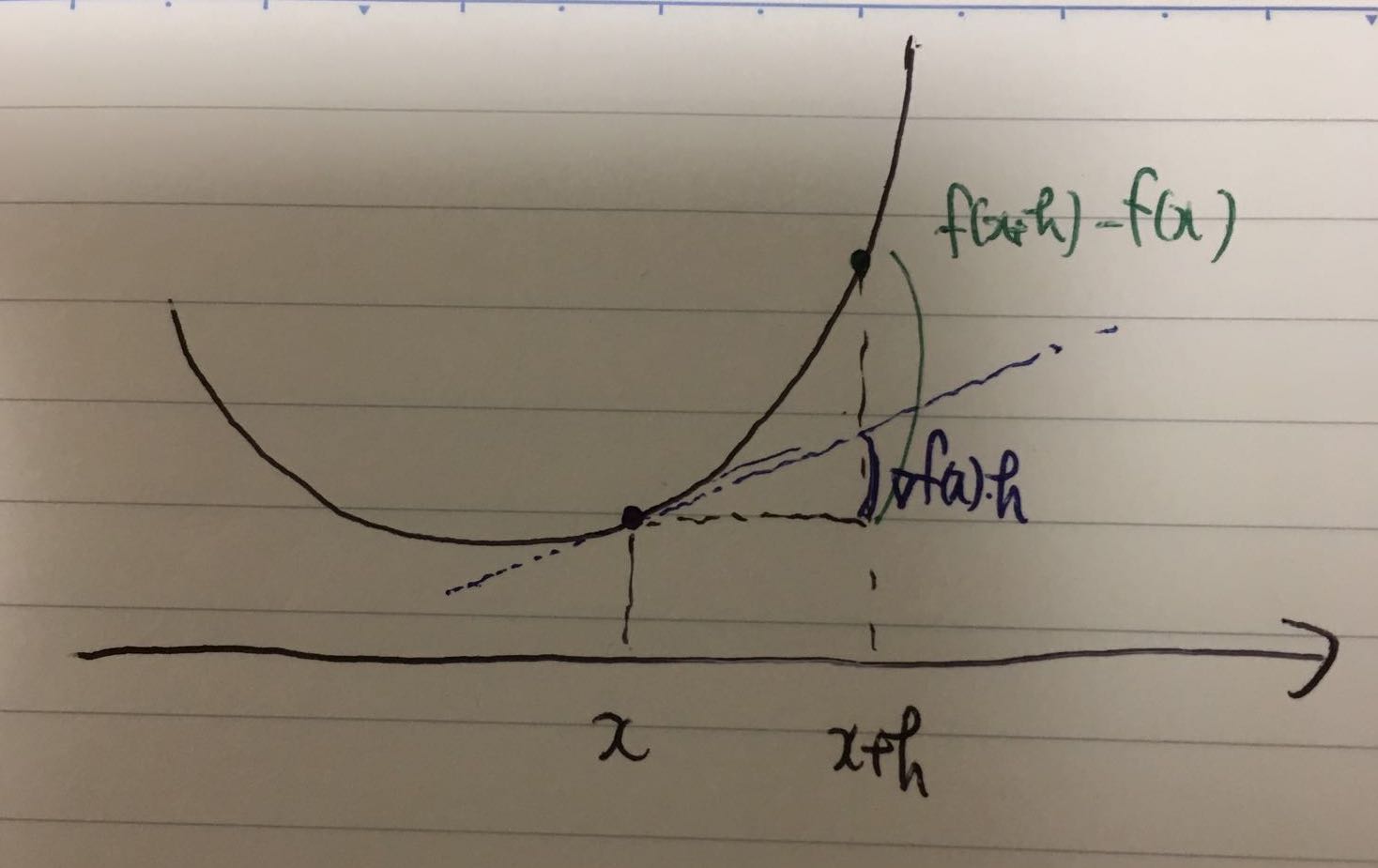
cpp-snip-wrong-result

要するに、狭義凸関数$f$上のある地点を通る接線は$f$以下の値を取る、ということを主張しているだけである。

次に、$f$について2次のテーラー展開を行うと、

\[f(x) = f(a) + \nabla f(a)^T(x - a) + \frac{1}{2}(x - a)^T Hf(c)(x - a)\ \ \ \ (\exists{c}, c\in {\lambda x + (1 - \lambda)y, 0\le \lambda \le 1}) \tag{3}\]

上式を満たすような$c$が存在することがわかる。なお、

\[Hf(c) = \begin{bmatrix} \frac{\partial}{\partial \theta_1 \partial \theta_1}&\dots&\frac{\partial}{\partial \theta_1 \partial \theta_n}\\ \vdots&\ddots&\vdots\\ \frac{\partial}{\partial \theta_n \partial \theta_1}&\dots&\frac{\partial}{\partial \theta_n \partial \theta_n}\\ \end{bmatrix} f(c)\]

である。$(3)$式を変形すると、

\[f(x) - f(a) + \nabla f(a)^T(x - a) = \frac{1}{2}(x - a)^T Hf(c)(x - a) > 0 \tag{4}\]

となる($(2)$式よりこの式は正であることがわかる)。 $(4)$式よりヘッセ行列は正定値行列であることがわかり、よって正則であることが示された。