スプライン関数
元の現象が連続的なものであっても、実験や統計の結果として得られるデータは離散的なものです。そのため、測定しなかった入力に対する出力が欲しい場合は、手元にある離散的なデータから推定する必要があります。
古典的な推定法としては、Lagrangeの補完法というものがあります。これは、$n$個の点$\{(x_i, y_i)\}_{i=1}^n,\ \ i\neq j \Rightarrow x_i \neq x_j$が与えられたときに多項式を用いてデータを推定するものです。具体的には、
\[P(x) = \sum_{i=1}^n y_ip_i(x)\\ p_i(x) = \prod_{j=1, j\neq i}^n \frac{x - x_j}{x_i - x_j}\]で表される$P(x)$が補間多項式となります。これは全てのデータ点${(x_i, y_i)}_{i=1}^n$を通る、$n-1$次の多項式です。
しかし、このような多項式による近似は良い近似にならない場合があります。例えば以下の例を見てみましょう。
> library('ggplot2')
> library('polynom')
> x <- seq(0, 10, by=1)
> y <- sin(x) + rnorm(11, sd=0.1)
> dat <- data.frame(cbind(x, y))
> poly.calc(x, y)
0.07066721 - 6.503391*x + 18.75596*x^2 - 18.35645*x^3 + 9.239577*x^4 - 2.754634*x^5 + 0.5117172*x^6 - 0.05956099*x^7 +
0.004201839*x^8 - 0.0001633528*x^9 + 2.667467e-06*x^10
> f <- function(x) {return(0.07066721 - 6.503391*x + 18.75596*x^2 - 18.35645*x^3 + 9.239577*x^4 - 2.754634*x^5 + 0.5117172*x^6 - 0.05956099*x^7 +
+ 0.004201839*x^8 - 0.0001633528*x^9 + 2.667467e-06*x^10)}
> ggplot(dat, aes(x=x, y=y)) + geom_point(size=5, col='blue') + stat_function(fun = f, size=1.25, alpha=0.4, xlim=c(-0.3, 10.3))
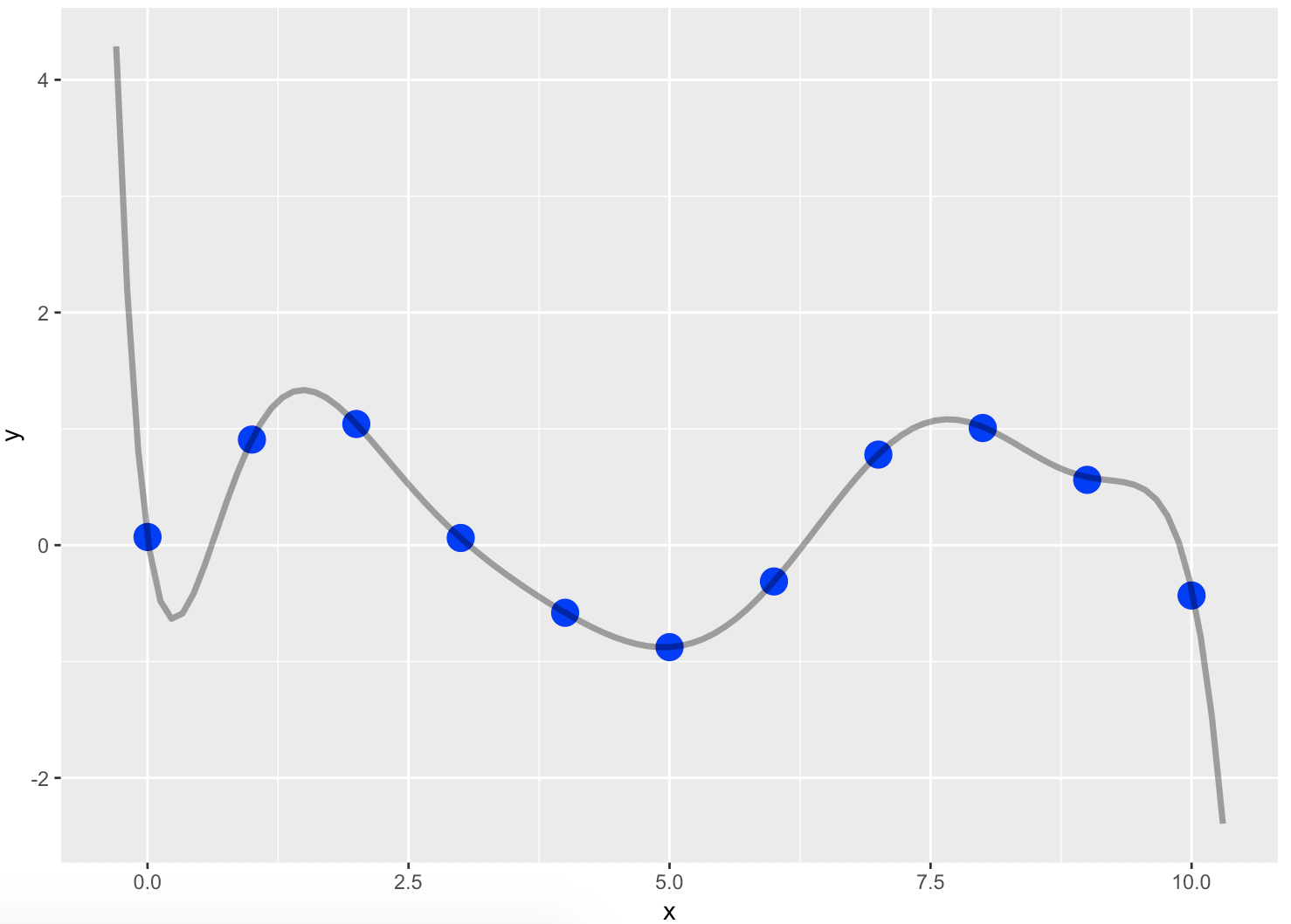
上の例はsinカーブにノイズを乗せた点11個からLagrange補間を行った結果を図示したものです。図のように、部分的には元の関数の振舞いを表現できていますが、特にデータの端よりも外にある範囲の補間(補外といいます)が全くおかしなことになっています。これはデータがない部分を表そうというのがそもそも難しいというのもあるのですが、それにしてももう少し上手いこと推定して欲しいところです。
Lagrange補間がデータの端より外にある範囲で変化が激しくなるのは、一つの多項式で全体を表そうとしたことが問題であると考えられます。そこで、単一の多項式によって補完するのではなく、ある範囲のときにだけ多項式になる関数 (区分的多項式) をいくつも用意し、それらを滑らかっぽく繋げることで補完しようというのがスプライン平滑化 (spline smoothing) の気持ちです。
区分多項式とスプライン
ここで用語の定義をしておきます。$a = \xi_0 < \xi_1 < \dots < \xi_n = b$となるような実数の増加列$\{\xi\}$を考え、$[a, b]$上の連続関数で各区間$[\xi_{i-1}, \xi_i]$に制限したときに多項式になるようなものを区分的多項式といいます。区分的多項式$P$は$n$個の多項式$p_0, \dots, p_{n-1}$を用いて、
\[P(x) = \begin{cases} p_0(x) & \xi_0 \le x < \xi_1 \\ \vdots & \\ p_{n-1}(x) & \xi_{n-1} \le x < \xi_n \\ \end{cases}\]と定義できます。また、区分的多項式の次数はこのように定義します。
\[\deg P := \max_{0 \le i \le n-1} \deg p_i\]つまり$n$個ある多項式のうちの最大次数を区分的多項式の次数にする、というわけです。
ここで、高々$k$次の区分的多項式で、$(a, b)$の範囲で$C^{k-1}$に属するものを高々$k$次のスプライン関数と呼び、$\{\xi_{i}\}$をノット、$\boldsymbol{\xi} = (\xi_1, \dots, \xi_{n-1})$をノットベクトルと呼びます。 つまり区分的多項式モデルの関数に$k-1$次の微分連続性を求めたものが$k$次のスプラインということです。
さらに、両端の外側に線形制約 (2次以上の項が存在しない) という条件をスプラインに課したものを自然スプラインといいます。$k$次のスプラインに外側に線形制約を課したものは$k$次の自然スプラインですね。
平滑化スプライン
回帰のテクニックとして、RidgeやLassoといった正則化項を導入してモデルが過度に複雑になることを防ぐ方法が知られています。今回はその正則化と同じように、回帰関数の曲率がなるべく小さくなるように関数を求めてみましょう。つまり、
\[\displaystyle \min_{f \in C^2}\sum_{i=1}^n (y_i - f(x_i))^2 + \lambda \int_a^b (f^{\prime\prime}(t))^2 dt, \ \ \lambda > 0 \tag{1}\]を解いてやればいいことになります。ここで$\lambda$は平滑化パラメータで、$\lambda$が大きいほど曲率が小さい関数が好まれるようになり、$\lambda \to \infty$で$f$は線形モデルになります。
さて、$(1)$の解はどのような関数になるでしょうか?実は、$\{x_i\}$をノットとする3次の自然スプラインになります。これを今から証明していきましょう1。なお、このスプラインを平滑化スプラインと呼びます。
(1)の解が3次自然スプラインになることの証明
$\tilde{g}(x)$を$(1)$の解とする。$\tilde{g}$が各$x_i$において通る点を$z_i = \tilde{g}(x_i)$とおく。一方、$g(x)$を$\{x_i\}$のノットとし、$\{x_i, z_i\}$を通るような3次自然スプラインとする。このような3次自然スプラインは自由度が$n$であることから必ず存在する。
このとき、全ての$x \in [a, b]$において$g(x) = \tilde{g}(x)$であることを示す。
$\tilde{g}(x)$は$(1)$式の解であることから、 \(\begin{align} \displaystyle \sum_{i=1}^n (y_i - \tilde{g}(x_i))^2 + \lambda \int_a^b (\tilde{g}^{\prime\prime}(t))^2 dt &\le \sum_{i=1}^n (y_i - g(x_i))^2 + \lambda \int_a^b (g^{\prime\prime}(t))^2 dt\\ \displaystyle \sum_{i=1}^n (y_i - z_i)^2 + \lambda \int_a^b (\tilde{g}^{\prime\prime}(t))^2 dt &\le \sum_{i=1}^n (y_i - z_i)^2 + \lambda \int_a^b (g^{\prime\prime}(t))^2 dt\\ \displaystyle \lambda \int_a^b (\tilde{g}^{\prime\prime}(t))^2 dt &\le \lambda \int_a^b (g^{\prime\prime}(t))^2 dt\\ \displaystyle \int_a^b \tilde{g}^{\prime\prime}(x)^2dx &\le \int_a^b g^{\prime\prime}(x)^2dx\ \ (\because \lambda > 0) \tag{2} \end{align}\)
を満たす。
次に、$\int_a^b \tilde{g}^{\prime\prime}(x)^2dx \ge \int_a^b g^{\prime\prime}(x)^2dx$を証明する。$h(x) := \tilde{g}(x) - g(x)$という関数$h$を考えると、
\[\begin{align} \tilde{g}^{\prime\prime}(x) &= h^{\prime\prime}(x) + g^{\prime\prime}(x)\\ \tilde{g}^{\prime\prime}(x)^2 &= h^{\prime\prime}(x)^2 + g^{\prime\prime}(x)^2 + 2h^{\prime\prime}(x)g^{\prime\prime}(x)\\ \int_a^b \tilde{g}^{\prime\prime}(x)^2 dx &= \int_a^b h^{\prime\prime}(x)^2 dx+ \int_a^b g^{\prime\prime}(x)^2 dx + 2\int_a^b h^{\prime\prime}(x)g^{\prime\prime}(x) dx \tag{3}\\ \end{align}\]$\int_a^b h^{\prime\prime}(x)g^{\prime\prime}(x) dx$について部分積分を行うと、
\[\displaystyle \int_a^b h^{\prime\prime}(x)g^{\prime\prime}(x) dx = [h^{\prime}(x)g^{\prime\prime}(x)]_a^b - \int_a^b h^{\prime}(x)g^{\prime\prime\prime}(x) dx\]$g$は自然スプラインなので、$g^{\prime\prime}$は両端では$0$になる。従って$(3)$の第一項は$0$である。
さらに、$g$は3次の区分的多項式なので、$g^{\prime\prime\prime}(x)$は各区間内で定数になる。そこで、区間$(x_j, x_j + 1)$における$g^{\prime\prime\prime}(x)$の値を$c_j$とおくと、
\[\begin{align} \int_a^b h^{\prime}(x)g^{\prime\prime\prime}(x) dx &= \sum_{j=1}^{n-1}c_j \int_{x_j}^{x_{j+1}}h^{\prime}(x)dx\\ &= \sum_{j=1}^{n-1}c_j [h(x)]_{x_j}^{x_{j+1}}\\ &= \sum_{j=1}^{n-1}c_j (h(x_{j+1}) - h(x_j))\\ &= \sum_{j=1}^{n-1}c_j (\tilde{g}(x_{j+1}) - g(x_{j+1}) - (\tilde{g}(x_{j}) - g(x_{j})))\\ &= \sum_{j=1}^{n-1}c_j (z_{j+1} - z_{j+1} - (z_j - z_j))\\ &= 0\\ \end{align}\]よって$(3)$式の第二項も$0$なので、$\int_a^b h^{\prime\prime}(x)g^{\prime\prime}(x) dx = 0$である。
\[\begin{align} \int_a^b \tilde{g}^{\prime\prime}(x)^2 dx &= \int_a^b h^{\prime\prime}(x)^2 dx+ \int_a^b g^{\prime\prime}(x)^2 dx + 2\int_a^b h^{\prime\prime}(x)g^{\prime\prime}(x) dx\\ &= \int_a^b h^{\prime\prime}(x)^2 dx+ \int_a^b g^{\prime\prime}(x)^2 dx\\ &\ge \int_a^b g^{\prime\prime}(x)^2 dx \tag{4}\\ \end{align}\]また、両辺が等しいので$h(x)$が全ての$x \in [a, b]$において$0$のときのみである。$(5)$
$(2)$, $(4)$より$\int_a^b \tilde{g}^{\prime\prime}(x)^2dx = \int_a^b g^{\prime\prime}(x)^2dx$。$(5)$に気をつけると、全ての$x \in [a, b]$について、
\[\tilde{g}(x) = g(x)\](証明終)
なお、$\lambda$は実際にはどうやって求めるかというと、一般化クロスバリデーション (GCV) という手法を使うことで求めるようです (この部分を勉強する余裕ができて理解できれば記事にします。。)。
Rでの実装例
最後にRで平滑化スプラインを行った例を確認してみましょう。今回使用する関数はmgcvというパッケージのgam関数で、gamはGeneralized Additive Model (一般化加法モデル) の略です。一般化加法モデルは平滑化スプラインの説明変数が複数になったバージョンのモデルですが、これを使って平滑化スプラインのモデルも表現できるのでこちらを使用します。
> library('mgcv')
> x <- seq(0, 10, by=1)
> y <- sin(x) + rnorm(11, sd=0.1)
> dat <- data.frame(cbind(x, y))
> gam.model <- gam(y ~ s(x), data=dat)
> plot(gam.model, residuals = T, pch = 19, col='black', xlim=c(-2, 12))
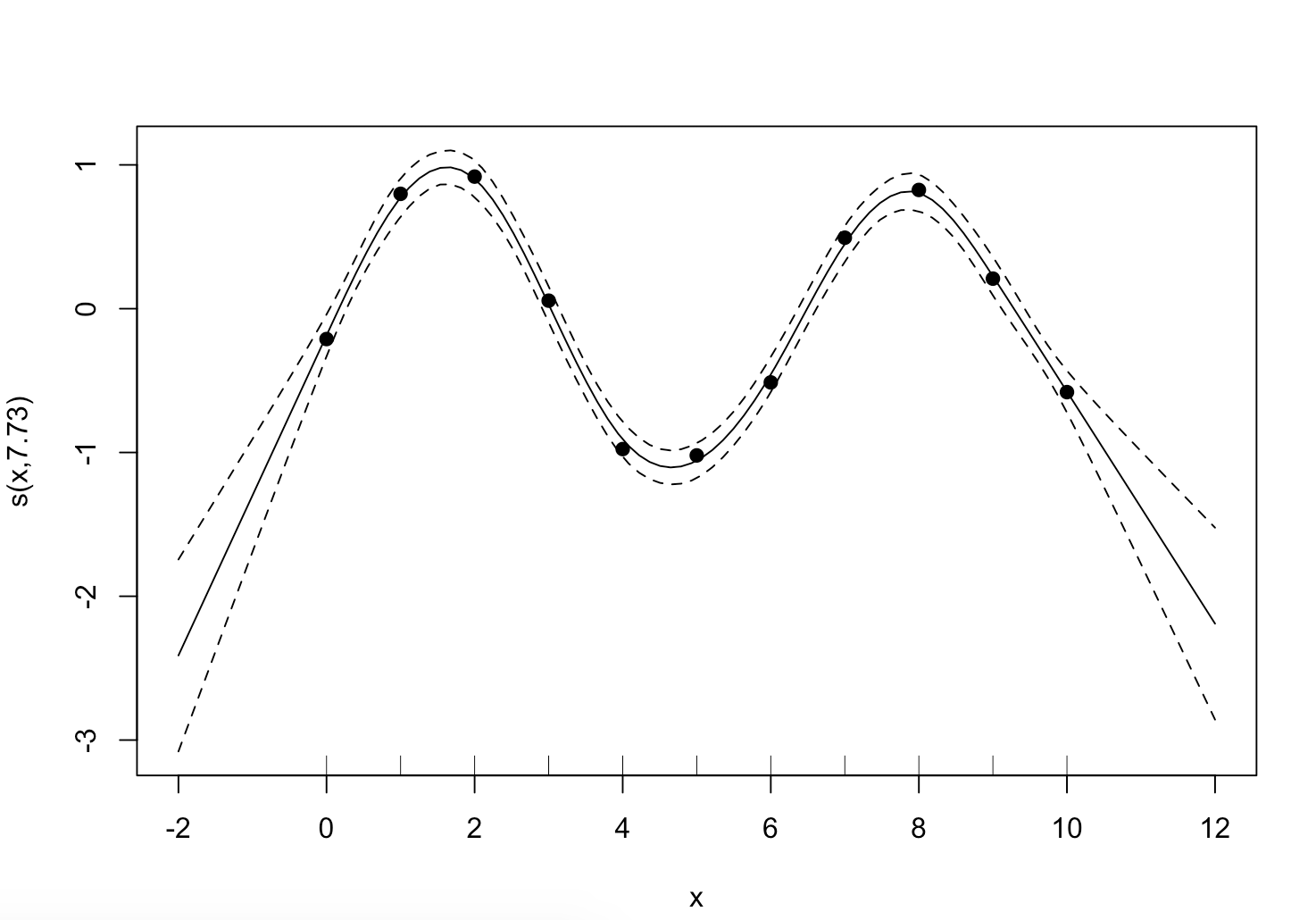
図のように、Lagrange補間がデータの端点の外側が11次式の項で急激に変化していたのに対し、平滑化スプラインでの補間は端点の外側が線形であることが保証されているので変化が比較的穏やかになりました。なお、実際のデータ解析では与えられたデータ点全てをノットに使うのではなく、適当な方法で間引いたものをノットとすることが多いようです2。
参考文献
1: 統計的学習の基礎 5章前半(~5.6)の証明ほぼそのままです
2: Thin-plate spline法に書いてありました