最近PuLPという線形計画問題 (や混合整数問題) を解くためのPythonライブラリを触ったのでそれの使い方をメモしておきます。
まず線形計画問題について簡単に説明をします。
線形計画問題とは
用語の復習から。
実数$c_1, \dots, c_n \in \mathbb{R}$に対して、次のように与えられる実変数$x_1, \dots, x_n$の関数
\[f(x_1, \dots, x_n) = c_1x_1 + \dots + c_nx_n\]を線形関数 (linear function) と呼びます。$f$が線形関数で、$b$が実定数のとき、
\[f(x_1, \dots, x_n) = b\]の関係式を線形等式 (linear equality) といい、
\[f(x_1, \dots, x_n) \ge b\]や
\[f(x_1, \dots, x_n) \le b\]の式を線形不等式 (linear inequality) といいます。
さて線形計画問題 (linear programming problem; LP)とは、有限個の線形等式または線形不等式を満たし、かつ与えられた線形関数を最大化 (最小化) する問題のことです。最大化 (最小化) する線形関数のことを目的関数 (objective function) といい、満たすべき線形等式・線形不等式のことを線形制約式、または線形制約条件 (linear constraint) とよびます。また、線形制約条件すべてを満たす解を実行可能解 (feasible solution) といい、その集合を実行可能領域 (feasible region) といいます。なお、実行可能領域が空集合でない問題を実行可能な問題といい、逆に実行可能領域が空集合である問題を実行不可能な問題であるといいます。1
実行可能解のうち目的関数を最大 (最小) にする解を最適解 (optimal solution) とよびます。
一つ例をあげてみましょう。
例題 (ダイエット問題)
(問題はこちらのサイトのものを数値だけ変えています。)
ある動物園では、飼育しているコアラが太ってしまったため糖質制限をかけた餌を与えてダイエットさせることにしました。コアラの主食であるユーカリには糖質の他にも食物繊維、ミネラル、毒素が含まれていますが、ミネラル以外のものは取りすぎると良くないので、これらにも摂取制限をかけます。 成分構成が異なる2つのユーカリの比を上手く変えることで、なるべく多くのミネラルを摂取させるにはどうすればよいでしょうか?
ユーカリ1gあたりの成分表 (成分の単位: mg)
| 成分 | ユーカリA | ユーカリB | 摂取上限 |
|---|---|---|---|
| 糖質 | 10 | 14 | 6400 |
| 食物繊維 | 12 | 10 | 6000 |
| 毒素 | 2.5 | 0.8 | 900 |
| ミネラル | 0.8 | 0.5 | – |
ミネラル摂取量の最大化が目的なので、ユーカリAのグラム数を$x$, ユーカリBのグラム数を$y$とおくと、目的関数である線形関数は、
\[\text{最大化:} \qquad 0.8x + 0.5y\]となります。
また、線形制約条件を式で表すと、
\[\begin{align} & \qquad & x &\ge 0\\ & \qquad & y &\ge 0\\ & \text{糖質:} \qquad & 10x + 14y &\le 6400\\ & \text{食物繊維:} \qquad & 12x + 10y &\le 6000\\ & \text{毒素:} \qquad & 2.5x + 0.8y &\le 900\\ \end{align}\]以上の制約条件を満たしながらミネラル摂取量を最大化することが今回の問題のゴールになります。
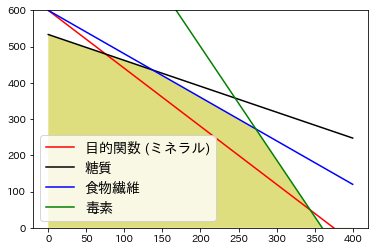
色がつけられた領域が実行可能領域であり、この中から目的関数を最大化する解を探索することになります。
PuLPによる問題の解法例
PuLPについて
PyPIのページには以下のように書かれています。
PuLP is an LP modeler written in python. PuLP can generate MPS or LP files and call GLPK, COIN CLP/CBC, CPLEX, and GUROBI to solve linear problems.
PuLPはLPを記述するためのモデラーであり、GLPKやCOINなどのソルバーは別に用意してAPIの形で呼び出します。2そのような設計になっているので、最適解を求めるソルバは付け替えができます (デフォルトではCOINというソルバを呼び出す)。
実際にソルバーが最適解を求める際には単体法 (Simplex Method) や内点法 (Internal Point Method) というアルゴリズムがよく使用されます。
それでは、先程の問題をPuLPを使って解いてみましょう。
コード
(ソースコードはgistに置いています。)
PuLP自体はpip install pulpでインストールできます。
まずはユーカリAとユーカリBについて、1mg当たりの糖質、食物繊維、毒素、ミネラルの含有量を変数に代入します。
import pulp
eucalyptus = ['a', 'b']
sugar_content = {
'a': 10,
'b': 14
}
fiber_content = {
'a': 12,
'b': 10
}
toxin_content = {
'a': 2.5,
'b': 0.8
}
mineral_content = {
'a': 0.8,
'b': 0.5
}
LpProblem()関数に引数を渡して最適化を解くためのオブジェクトを生成します。
引数の1つ目は問題の名前で、
2つ目は最大化か最小化かを示すためにLpMaximizeかLpMinimizeを渡してやります。
prob = pulp.LpProblem('Diet Problem', pulp.LpMaximize)
制約問題の変数を作成します。LpVariable()関数で変数一つずつ作ることもできますが、今回はLpVariable.dicts()で一気に作成をします。lowBoundで変数が取る定義域の下限を指定できます。
eucalyptus_vers = pulp.LpVariable.dicts('Eucalyptus', eucalyptus, lowBound=0)
目的関数を先程作成したprobオブジェクトに追加します。これは(目的関数, 目的関数の説明)のtupleを+演算子でLpProblemのオブジェクトに作用させることで表現できます。今回は0.8x + 0.5yが目的関数なので以下のように表すことができます。
prob += pulp.lpSum([mineral_content[i] * eucalyptus_vers[i] for i in eucalyptus]), 'Total Mineral Content'
制約条件も同じようにprobオブジェクトに+で追加できます。
prob += pulp.lpSum([sugar_content[i] * eucalyptus_vers[i] for i in eucalyptus]) <= 6400, 'Total Sugar Content'
prob += pulp.lpSum([fiber_content[i] * eucalyptus_vers[i] for i in eucalyptus]) <= 6000, 'Total Fiber Content'
prob += pulp.lpSum([toxin_content[i] * eucalyptus_vers[i] for i in eucalyptus]) <= 900, 'Total Toxin Content'
solve()を呼び出すことで最適化をソルバが解いてくれます。
prob.solve()
solve()を呼び出した後、最適解が得られているかは以下のコードを実行すれば確認できます。
pulp.LpStatus[prob.status]
出力が'Optimal'ならば最適解が得られています。
解の出力は以下。
for v in prob.variables():
print(f'{v.name} = {v.varValue}')
print(prob.objective)
print(f'optimized value: {pulp.value(prob.objective)}')
output:
Eucalyptus_a = 277.03704
Eucalyptus_b = 259.25926
0.8*Eucalyptus_a + 0.5*Eucalyptus_b
optimized value: 351.25926200000004
一応、最適解が得られているか図示して確認しましょう。
def plot_feasible_region(obj_value: float):
x = np.arange(0,400,0.01)
y0 = 0 * x
y1 = - 5 / 7 * x + 1600 / 3
y2 = - 6 / 5 * x + 600
y3 = - 25 / 8 * x + 1125
y_obj = -1.6 * x + 2 * obj_value
y = np.minimum(np.minimum(y1, y2), y3)
plt.plot(x, y_obj, color='r', label='目的関数 (ミネラル)')
plt.plot(x, y1, color='k', label='糖質')
plt.plot(x, y2, color='b', label='食物繊維')
plt.plot(x, y3, color='g', label='毒素')
plt.fill_between(x, y0, y, facecolor='y', alpha=0.5)
plt.ylim(0, 600)
plt.legend(prop={'size': 14})
plot_feasible_region(pulp.value(prob.objective))
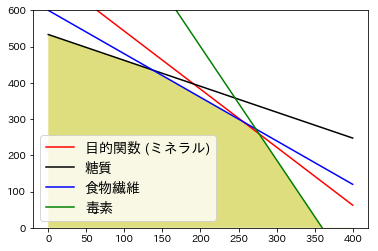
目的関数が実行可能領域を通る中で$y$切片が一番大きい値になっていることが分かります。たしかに最適な値を出力できていることが確認できました。
補足
問題に等号のない不等式を含む場合は線形計画問題とは呼びません。これは例をみると理由がすぐわかって、以下の簡単な問題
\[\text{最大化: } x_1\\ \text{条件: } x_1 < 5\]でも、$x_1 = 5$が実行可能領域ではないため最適解を得られない事態が発生するためです。
なお、PuLPは非線形計画問題は解けないので、目的関数や制約条件に非線形な式を入れようとするとエラーを返します。
# 0.2 * x * y == 100 の制約条件
prob += 0.2 * eucalyptus_vers['a'] * eucalyptus_vers['b'] == 100, 'Dummy Non-Linear Constraiant'
出力:
TypeError: Non-constant expressions cannot be multiplied
参考
- pulp: Pulp classes — PuLP 1.6.0 documentation
- Python+PuLPによるタダで仕事に使える数理最適化
- PuLP: A Linear Programming Toolkit for Python
- COIN-OR: Computational Infrastructure for Operations Research – Open-source Software for the Operations Research Community
- 線形計画問題
- 線形計画問題 (東京工業大学 大学院社会理工学研究科 経営工学専攻)
実行可能な問題でも最適解が存在しない場合もあり、そのような問題は非有界 (unbounded) であるというそうです。それ以外の問題は有界 (bounded) であるといい、LPが最適解を持つことは「問題が実行可能かつ有界」であることと同値のようです。
非線形計画問題を解きたかったらPyomoとか別のパッケージもあるらしい