年末年始の休みでRustを触っており、勉強がてら線形回帰を実装してみた。
線形回帰
まずは線形回帰について簡単に解説しておく。PRMLの3.1節を参考にした。
回帰は連続量である目的変数 $y$ を $d$ 次元の説明変数 $x = (x_1, \dots, x_D)^\text{T} \in \mathbb{R}^d$ を使って予測することである。パラメータ $w’ = (w’_0, \dots, w’_D)^\text{T} \in \mathbb{R}^{d+1}$ を用いると、線形回帰を表すモデル $y$ は
\[y(x, w') = w'_0 + \sum_{i=1}^d w'_ix_i \tag{1}\]のように表せる (ここでは $y \in \mathbb{R}$ としている)。ただし $(1)$ 式のように入力に対して線形の場合モデルに大きな制限がかかるので、 $x$ に非線形関数 (基底関数, basis function) $\phi$ をかけて
\[y(x, w) = w_0 + \sum_{j=1}^{M-1} w_j\phi_j(x) = w^\text{T}\phi(x) \tag{2}\]の形にモデルを拡張することで表現力を持たせることもある。ここで $w = (w_0, \dots, w_{M-1})^\text{T} \in \mathbb{R}^M$, $\phi = (\phi_0, \dots, \phi_{M-1})^\text{T}: \mathbb{R}^M \to \mathbb{R}^M$ であり、 $\phi_0(x) = 1$ としている。$(2)$ 式もパラメータに対して線形であることから線形回帰モデルとよぶ。
ここで、目的変数 $t$ が回帰モデルにガウシアンノイズを足した形、
\[t = y(x, w) + \epsilon\]で表せると仮定する。損失関数としてサンプルサイズが $N$ のデータセット $D$ に対するモデルの平均二乗誤差 $E_D[w]$ を考え、この誤差を最小にする線形回帰モデルのパラメータ $w_\text{ML}$ を求める。 平均二乗誤差が $w$ に対して凸であることから、
\[E_D[w] = \frac{1}{2}\sum_{n=1}^N \{t_n - w^\text{T}\phi(x_n)\}^2\]を $w$ について微分して $0$ となる点を求めればよいので、
\[0 = \sum_{n=1}^N t_n\phi(x_n)^\text{T} - w^\text{T}\left(\sum_{n=1}^N\phi(x_n)\phi(x_n)^\text{T}\right)\]から
\[w_\text{ML} = (\Phi^\text{T}\Phi)^{-1}\Phi^\text{T}t \tag{4}\] \[\left( \Phi := \begin{bmatrix} \phi_0(x_1) & \phi_1(x_1) & \dots & \phi_{M-1}(x_1) \\ \phi_0(x_2) & \phi_1(x_2) & \dots & \phi_{M-1}(x_2) \\ \vdots & \vdots & \dots & \vdots \\ \phi_0(x_N) & \phi_1(x_N) & \dots & \phi_{M-1}(x_N) \\ \end{bmatrix} \right)\]となることが分かる。データセットに対する平均二乗誤差を最小にするパラメータ $w_\text{ML}$ を得られたので、予測時は入力 $x_*$ に対して
\[y_* = w_\text{ML}\phi(x_*)\]のように目的変数 $y_*$ を計算すればよい。
Rustコード
上で述べたものを愚直に実装していく。ただし、今回は簡単のため $x$ の次元を1次元に限定した。
pub struct LinearRegression {
coefficients: Array1<f64>,
phi_x: Array2<f64>,
}
impl LinearRegression {
pub fn fit<'a>(
x: ArrayView1<f64>,
t: ArrayView1<f64>,
f: Box<dyn Fn(f64) -> Vec<f64>>,
) -> Result<LinearRegression, Box<dyn std::error::Error>> {
let phi = |v| {
let mut vec = vec![1.0];
vec.append(&mut f(v));
vec
};
let col = phi(f64::NAN).len();
let phi_x = Array2::from_shape_vec(
(x.len(), col),
x.to_vec().into_iter().flat_map(phi).collect::<Vec<_>>(),
)
.unwrap();
let w = phi_x.t().dot(&phi_x).solve(&phi_x.t().dot(&t)).unwrap();
Ok(LinearRegression {
coefficients: w,
phi_x,
})
}
pub fn predict(&self) -> Array1<f64> {
self.phi_x.dot(&self.coefficients)
}
}
LinearRegression::fit に引数として $x$ と $t$, および定数部分を除いた基底関数 $f$ を与えて $(w_\text{ML}, \phi(x))$ の組を返す仕組みにした。ただし基底関数の定数部分は fit 内で追加するような形にしている。最初は $w$ を求めるのにムーア・ペンローズ一般逆行列 ($(4)$ 式の $(\Phi^\text{T}\Phi)^{-1}\Phi^\text{T}$) を計算していたが、逆行列の計算コストは重いので連立方程式の解を直接出すように変更した。
src/bin/linear_regression.rs からライブラリを呼び出す。
fn main() {
run(Box::new(|v| vec![v]), "linear", "Linear");
}
のように基底関数と可視化用の画像タイトル、出力画像名を与えて $\sin x$ に対する線形モデルによる予測結果の画像を出力する。 以下はそれぞれ基底関数を線形、3次多項式、ガウシアンの3パターンでの結果。ガウシアンでは分散が同じで平均が異なる関数を5つ重ねている。赤線がモデルによる出力、緑線が目的関数の $\sin x$。
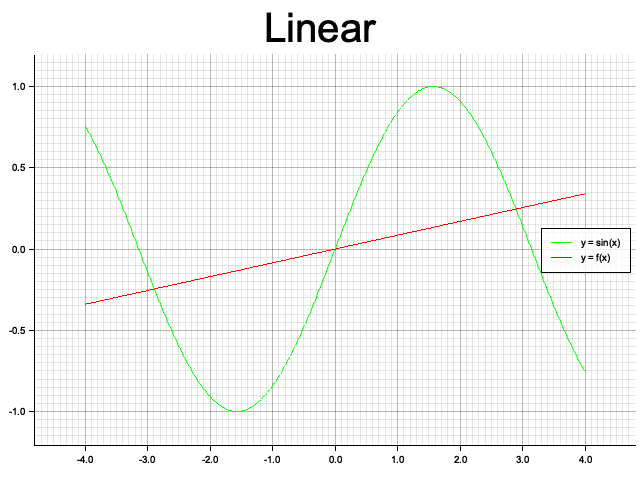
線形
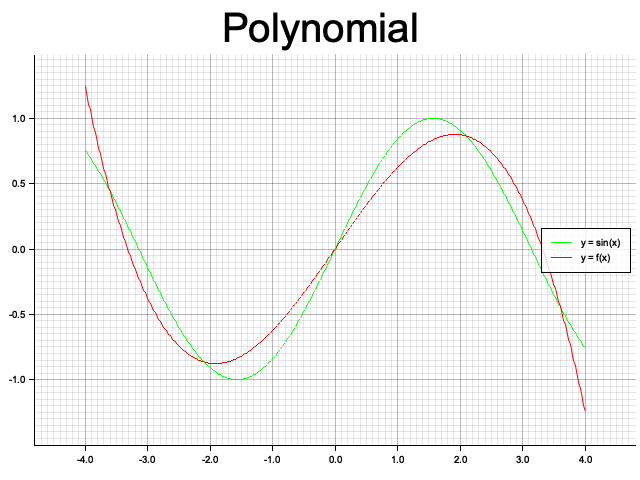
3次多項式

ガウシアン
感想
今は自分がthe bookを一通り終わらせただけで言語に慣れていないせいだろうが、正直まだ書きにくいイメージがある。とくに言語が提供する標準ライブラリが小さく、rand関数や数値系のトレイトもライブラリを追加する必要があるのは抵抗がある。
ただ実行速度が速いとか、所有権と借用というシステムを導入することでrace conditionが起こりにくくなっているとかのメリットは分かるのでもう少し触って様子を見ていきたい。
補足
可視化ライブラリに plotters を使っているが、自分の環境 (バージョン: 0.3.1) では先に出力先のディレクトリを生成しておかないとエラーも吐かず裏で失敗しており時間取られた (ref: 38/plotters_#236)。
参考文献
Christopher M. Bishop, Pattern Recognition and Machine Learning, Springer, 2006, pp.138-143